2.1 THE TOOTH

The toothed gears perform power transmission between rigid bodies through the interaction of teeth progressively in contact. The circumference along which the contact between the two toothed gears takes place is referred to as the pitch circle. The distance between the centers of the pitch circles that constitute a pair of gears is called the operating distance.

The teeth can have different types of profile. The most widespread profiles have the shape of an involute, a curve obtained as the trajectory of a point belonging to a line that rolls without sliding on a circumference.

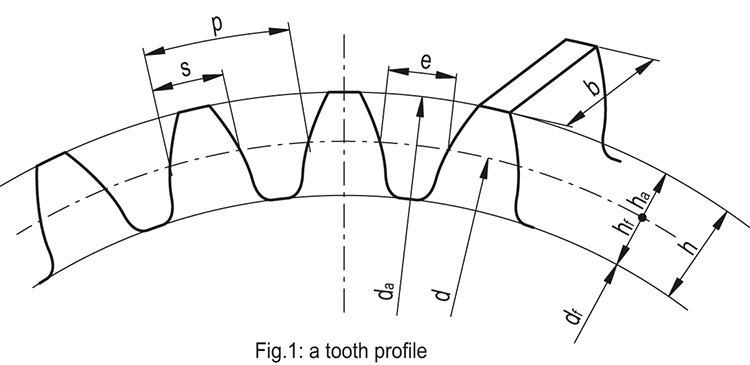
Commonly, the teeth develop in a radial direction straddling the pitch surface. The top land is defined as the part protruding from the pitch surface and included between the pitch circle and the addendum circle. The part between the pitch circle and the root circle is called the bottom land. Each of the tooth's side surfaces is called a profile. It is divided into two portions from the pitch circle: the external portion is called the face of the tooth, the internal portion is called the flank of the tooth.

The profile of a tooth (Fig.1) can be divided into two parts: the addendum (h_a) is defined as the distance in the radial direction between the pitch circle (d) and the addendum circle (d_a); the dedendum (h_f) is defined as the distance, also radial, between the pitch circle and the root circle (d_f), which delimits the tooth bottom. The sum of these two sizes constitutes the height of the tooth (h).

The circular pitch (p) is defined as the distance between two homologous points of two consecutive teeth, measured along the pitch circle. The space width (e) is the length of the arc of the pitch circle between two consecutive teeth. The tooth thickness (s) is the length of the pitch circle arc limited by a tooth. Finally, the face width (b) is defined as the axial size of the tooth.

In order to mesh correctly, the two toothed gears, with a radius of the pitch circle equal to r₁ and r₂, have the same pitch p. The circular pitch is therefore linked to the pitch circle by the following relation:

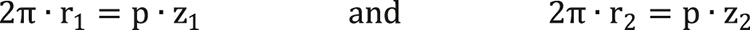
where z is the number of teeth present on the gear. From here, a fundamental measure can be obtained for the use of the toothed gears, ie the module (m):

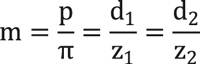
To mesh correctly with each other, two gears must have the same pitch (p), hence they must also have the same module (m).

The number of teeth can also be related to the transmission ratio (τ) by the following formula:

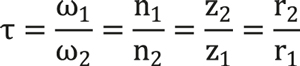
Another necessary condition for two gears to mesh is that they have the same angle of inclination of the helix. The teeth of the driving gear transmit to the teeth of the driven wheel a force (F) which has a direction such as to form a pressure angle (α) with the tangent common to the two pitch circles. The value of the pressure angle (α) influences the minimum number of teeth that a gear can have so that the whole tooth profile has an involute shape. ELESA transmission elements have pressure angles of 20°.